3. Vectors

• A vector is a quantity having both magnitude and direction.
  e.g.: velocity, force, acceleration.

  It is represented by an arrow over the mathematical symbol, or in bold face. For example, \(\vec{F}\) or as \(\boldsymbol{F}\), are used for force.

• A scalar is a quantity having magnitude but no direction.
  e.g.: length, time, temperature.

• A vector \(\vec{a}\) in a three dimensional real space expressed in terms of \(x,y,z\) components is: \[\vec{a} = a_1\vec{\imath} + a_2 \vec{\jmath} + a_3 \vec{k}\] where \(a_1\vec{\imath}, a_2\vec{\jmath},\) and \(a_3\vec{k}\) are vectors which lie along the coordinate axes \(x,y\), and \(z\) respectively, and have their origin at a common initial point.

  The magnitude, length, or norm of a vector \(\vec{a}\), as denoted by \(|\vec{a}|\) is: \[|\vec{a}| = \sqrt{a_1^2+a_2^2+a_3^2}\]

• Unit vector is denoted with a hat (i.e., \(\hat{\ }\)) symbol. To find the unit vector (\(\hat{a}\)) in the direction of \(\vec{a}\), simply divide the vector by its magnitude. \[\hat{a} = \frac{\vec{a}}{|\vec{a}|}\] The unit vectors in \(x,y,z\) directions are given as \(\hat{\imath}, \hat{\jmath}, \hat{k}\). They are also given simply as \(\vec{\imath}, \vec{\jmath}, \vec{k}\).

• Vector addition or subtraction: \[\begin{aligned} \vec{a} + \vec{b} &= (a_1 + b_1)\vec{\imath} + (a_2+b_2)\vec{\jmath} + (a_3+b_3)\vec{k} \\ \vec{a} - \vec{b} &= (a_1 - b_1)\vec{\imath} + (a_2-b_2)\vec{\jmath} + (a_3-b_3)\vec{k}\end{aligned}\]

• Vector multiplication: There are two types of multiplication.

  • Dot product: \[\vec{a}\cdot \vec{b} = |\vec{a}||\vec{b}|\cos(\theta) = a_1b_1 + a_2b_2 + a_3b_3\] where \(\theta\) is the angle between the vectors, such that \(0\le \theta \le \pi\). The dot product yields a scalar answer.

    • Dot product is also called as scalar product or inner product.

    • Dot product is commutative. i.e., \[\vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{a}\]

    • If \(\vec{a}\cdot\vec{b}=0\), with \(|\vec{a}|\ne 0\), and \(|\vec{b}|\ne 0\), then the vectors are orthogonal (perpendicular) to each other.

    • If vectors \(\vec{a}\) and \(\vec{b}\) are parallel, then \[\vec{a}\cdot\vec{b} = |\vec{a}|\cdot|\vec{b}|\]

    • For the unit vectors \(\vec{\imath}, \vec{\jmath}\) and \(\vec{k}\) \[\vec{\imath}\cdot\vec{\imath} = \vec{\jmath}\cdot\vec{\jmath} = \vec{k}\cdot\vec{k} = 1\] and, \[\vec{\imath}\cdot\vec{\jmath} = \vec{\jmath}\cdot\vec{\imath} = \vec{\imath}\cdot{k} = \vec{k}\cdot\vec{\imath} = \vec{\jmath}\cdot{\vec{k}} = \vec{k}\cdot{\vec{\jmath}} = 0\]

  • Cross product: \[\vec{a}\times\vec{b} = |\vec{a}||\vec{b}|\sin(\theta)\vec{n}\] where \(\theta\) is the angle between the vectors, such that \(0\le \theta \le \pi\), and \(\vec{n}\) is a unit vector perpendicular to the plane of \(\vec{a}\) and \(\vec{b}\).

    • Cross product is also known as vector product.

    • A convenient method for computing the cross product is: \[\vec{a} \times \vec{b} = \begin{vmatrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} = (a_2b_3-b_2a_3)\vec{\imath} - (a_1b_3-b_1a_3)\vec{\jmath} + (a_1b_2-b_1a_2)\vec{k}\]

    • The following laws are valid: \[\begin{aligned} \vec{a}\times\vec{b} &= -\vec{b}\times\vec{a} \qquad (\text{commutative law for cross product fails!}) \\ \vec{a}\times(\vec{b}+\vec{c}) &= \vec{a}\times\vec{b} + \vec{a}\times\vec{c} \qquad (\text{distributive law})\end{aligned}\]

    • Two nonzero vectors \(\vec{a}\) and \(\vec{b}\) are parallel if and only if \(\vec{a}\times\vec{b}=0\)

    • For the unit vectors \(\vec{\imath}, \vec{\jmath}\) and \(\vec{k}\) \[\vec{\imath}\times\vec{\imath} = \vec{\jmath}\times\vec{\jmath} = \vec{k}\times\vec{k} = 0\] and, \[\begin{gathered} \vec{\imath}\times\vec{\jmath} = \vec{k}, \qquad \vec{\jmath}\times\vec{\imath} = -\vec{k}, \qquad \vec{\jmath}\times\vec{k} = \vec{\imath}, \qquad \vec{k}\times\vec{\jmath} = -\vec{\imath}, \qquad \\ \vec{k}\times{\vec{\imath}} = \vec{\jmath}, \qquad \vec{\imath}\times\vec{k} = -\vec{\jmath}\end{gathered}\]

• Vector Differentiation: Consider a vector \(\vec{r}\) which is a function of \(u\). i.e., \[\begin{aligned} \vec{r}(u)&=x(u)\vec{\imath}+y(u)\vec{\jmath}+z(u)\vec{k} \\ \frac{d\vec{r}}{du} &= \frac{dx}{du}\vec{\imath} + \frac{dy}{du}\vec{\jmath} + \frac{dz}{du}\vec{k}\end{aligned}\]

• The Del Operator (\(\nabla\)): It is also known as ‘vector-differential operator’. \[\nabla = \hat{\imath}\frac{\partial}{\partial x} + \hat{\jmath}\frac{\partial}{\partial y} + \hat{k}\frac{\partial}{\partial z}\]

• Gradient (\(\nabla f\)): where \(f\) is a scalar function. \[\nabla f = \hat{\imath}\frac{\partial f}{\partial x} + \hat{\jmath}\frac{\partial f}{\partial y} + \hat{k}\frac{\partial f}{\partial z}\]

  • Directional Derivatives: If \(\hat{n}\) is a unit vector, then \(\hat{n}\cdot \nabla f\) is called the directional derivative of \(f\) in the direction \(\hat{n}\). The directional derivative is the rate of change of \(f\) in the direction \(\hat{n}\).

  • Unit Normal to a Surface: If the surface \(S\) is given by the equation \(f(x, y, z) = 0\), then the unit normal at any point of the surface is simply given by \[\hat{n} = \frac{\nabla f}{|\nabla f|}\]

• Divergence \[\text{div} = \nabla \cdot\] The divergence of a vector field \(\vec{v}\) is given by \[\nabla\cdot\vec{v} = \frac{\partial v_1}{\partial x} + \frac{\partial v_2}{\partial y} + \frac{\partial v_3}{\partial z}\] where \(\vec{v} = v_1\vec{\imath} + v_2\vec{\jmath} + v_3\vec{k}\).

  • Divergence is a scalar.

  • Divergence is “flux density”—the amount of flux entering or leaving a point. It is the rate of flux expansion (positive divergence) or flux contraction (negative divergence).

  • For a flowing fluid with velocity vector \(\vec{v}\), the condition for incompressibility is given by \[\nabla\cdot \vec{v} = 0\]

• Curl \[\text{curl} = \nabla \times\] For a vector \(\vec{v}=v_1\vec{\imath}+v_2\vec{\jmath}+v_3\vec{k}\), \[\text{curl}(v) = \nabla \times \vec{v} = \begin{vmatrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ v_1 & v_2 & v_3 \end{vmatrix}\]

  • The curl is a function that measures the amount of “rotation” of a vector field.

  • A vector field \(\vec{v}\) is said to be irrotational if \({\text{curl}}(\vec{v})=0\).

• Laplacian operator (\(\nabla^2\)) \[\nabla^2=\frac{\partial^2}{\partial x^2}+ \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\]

• The curl of a gradient (of \(\phi\)) is zero. \[\nabla \times (\nabla\phi) = 0\]

• The divergence of a curl (of \(\vec{A}\)) is zero. \[\nabla \cdot (\nabla\times\vec{A}) = 0\]

• Line Integrals: For the vector \(\vec{a}\) in terms of its Cartesian components, \[\vec{a} = a_x\vec{\imath} + a_y\vec{\jmath}+a_z\vec{k}\] The integral of tangential component of \(\vec{a}\) along \(C\), called as line integral of \(\vec{a}\) is given by \[\begin{aligned} \int_{C}\vec{a}\cdot d\vec{r} &= \int_{C}(a_x\vec{\imath}+a_y\vec{\jmath}+a_k\vec{k})\cdot(dx\vec{\imath}+dy\vec{\jmath}+dz\vec{k}) \\ &= \int_C(a_xdx + a_ydy + a_zdz) \\ &= \int_Ca_xdx+\int_Ca_ydy + \int_Ca_zdz\end{aligned}\]

  • Reversing the path of integration changes the sign of the integral. \[\int_{A}^B\vec{a}\cdot d\vec{r} = -\int_{B}^A\vec{a}\cdot d\vec{r}\]

  • If the path of integration is subdivided into smaller segments, then the sum of the separate line integrals along each segment is equal to the line integral along the whole path. \[\int_{A}^B\vec{a}\cdot d\vec{r} = \int_{A}^P\vec{a}\cdot d\vec{r} + \int_{P}^B\vec{a}\cdot d\vec{r}\]

  Green’s Theorem

  

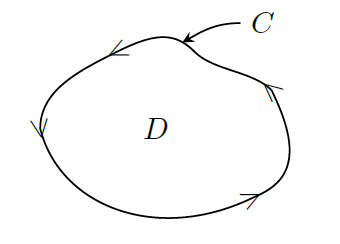
  Let \(C\) be a positively oriented (traced in counter-clockwise direction), piecewise smooth, simple, closed curve and let \(D\) be the region enclosed by the curve. If \(M\) and \(N\) have continuous first order partial derivatives on \(D\) then, \[\oint_C (M\,dx + N\,dy) = \iint_{D}\left(\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}\right)dx\,dy\] If we traverse the path following the positive orientation the region \(D\) must always be on the left.