Distillation

A solution of ethyl alcohol containing 8.6% alcohol by weight is fed at the rate of 5000 kg/hr to a continuous fractionating column operating at atmospheric pressure. The distillate which is the desired product contains 95.4% alcohol by weight and the residue from the bottom of the column contains 0.1% alcohol by weight. Calculate the following:

1. the mass flow rates of the distillate and residue in kg/hr, and
2. the percentage loss of alcohol.

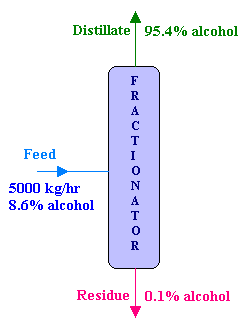
Overall material balance:

Feed = Distillate + Residue

i.e., F = D + R

D + R = 5000   → 1

Component balance for Alcohol:

Fx_F = Dx_D + Rx_R

Where x 's are the mole fraction of alcohol in various streams.

0.954 D + 0.001 R = 5000 x 0.086 = 430   → 2

Equations 1 and 2 contains 2 unknowns D and R, and that can be solved as follows:

Multiplying equation 1 by 0.001,

0.001D + 0.001 R = 5   → 3

subtracting equation 3 from equation 2,

0.953 D = 425

D = 446 kg/hr

i.e., Distillate flow rate = 446 kg/hr

Therefore, R = 5000 - 446 = 4554 kg/hr

i.e., Residue flow rate = 4554 kg/hr

Ethanol leaving in the residue (i.e., ethanol lost) = 4554 x 0.001 = 4.554 kg/hr

Ethanol entering in the feed = 5000 x 0.086 = 430 kg/hr

Percentage loss of ethanol = 100 x (4.554 / 430) = 1.06