Isothermal-Isochoric Process

One mole of an ideal gas, initially at 20^oC and 1 bar, undergoes the following mechanically reversible changes. It is compressed isothermally to a point such that when it is heated at constant volume to 100^oC its final pressure is 10 bar. Calculate Q, W, ΔU, and ΔH for the process. Take C_p = 7R/2 and C_v = 5R/2.

Calculations:

The given process is represented in PV diagram as follows:

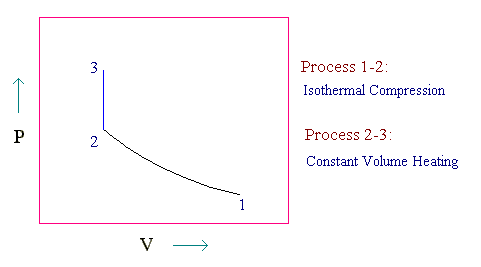
We can find the pressure and volume of points 1, 2 and 3 by equation of state (ideal gas equation)

For one mole of ideal gas,

P₁V₁ = RT₁

P₂V₂ = RT₂

P₃V₃ = RT₃

For the given process, T₂ = T₁ and V₃ = V₂.

V₁ = R x (273 + 20)/1 = 293R

And V₃ = R x (273 + 100) / 10 = 37.3R

For the point 2, P₂ = R x (273 + 20) / (37.3R) = 293/37.3 = 7.855 bar

PVT conditions of the points 1,2 and 3's are:

For the isothermal process:

ΔU = 0

ΔH = 0

W = ∫PdV = ∫RT dV/V = RT ln (V₂/V₁) = R x 293 x ln (37.3/293) = -604R

Q = -W = 604R (since Q + W = ΔU)

Work is done on the system and heat is given out by the system

For the constant volume heating (isochoric process):

W = 0

ΔU = C_v(T₃ - T₂) = (5R/2) x (373 - 293) = 200R

ΔH = C_p(T₃ - T₂) = (7R/2) x (373 - 293) = 280R

Q = ΔU - W = 200R

Summary: