Rate of Vaporization of Oxygen Stored in Insulated Sphere

A steel sphere is of inner diameter 40 cm and outer diameter 45 cm is used to store liquid oxygen (B.P is minus 183^oC). The sphere is covered with one layer of insulation, of thickness 50 mm whose K is 0.35 W/m.K and another insulation, of thickness 50 mm whose K is 0.098 W/m.K. The sphere is exposed to atmosphere of 25^oC. Find out the rate of oxygen becoming vapor every minute. Latent heat of oxygen is 370 kJ/kg. Thermal conductivity of steel = 20 W/m.K. Heat transfer coefficient of ambient air = 80 W/m².K

Calculations:

For composite concentric sphere, the rate of heat transfer from outside to the sphere Q, is given by,

Q = (T_a - T_b)/R

T_a = 25^oC

T_b = -183^oC

Where, R = R_s + R_ins,1 + R_ins,2 + R_a

R_a = air film resistance = 1 / (4πr_a²h_a)

R_ins,2 = Resistance offered by the outer insulation = (r_a - r₁) / (4πk_ins,2r_ar₁)

R_ins,1 = Resistance offered by the inner insulation = (r₁ - r₂) / (4πk_ins,1r₁r₂)

R_s = Resistance offered by the metal wall (steel) = (r₂ - r_b) / (4πk_sr₂r_b)

Given Data:

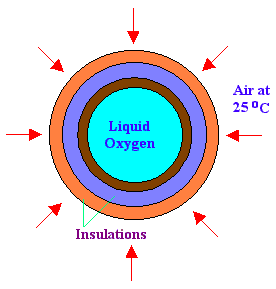
Diameter of sphere with insulation = 45 + 2 x 5 + 2 x 5 = 65 cm

r_a = 32.5 cm = 0.325 m

r₁ = 32.5 - 5 = 27.5 cm = 0.275 m

r₂ = 27.5 - 5 = 22.5 cm = 0.225 m

r_b = 20 cm = 0.2 m

Substituting these data in the above equations,

R_a = 1/(4 x 3.142 x 0.325² x 80) = 9.4175 x 10^-3 oC/W

R_ins,2 = (0.325 - 0.275)/(4 x 3.142 x 0.098 x 0.325 x 0.275) = 0.4543 ^oC/W

R_ins,1 = (0.275 - 0.225)/(4 x 3.142 x 0.35 x 0.275 x 0.225) = 0.1837 ^oC/W

R_s = (0.225 - 0.2)/(4 x 3.142 x 20 x 0.225 x 0.2) = 2.2105 x 10^-3 oC/W

R = 9.4175 x 10^-3 + 0.4543 + 0.1837 + 2.2105 x 10^-3 = 0.6496 ^oC/W

Q = (25 + 183)/0.6496 = 320.2 W

Rate of heat in per second = 320.2 J

Rate of heat in per minute = 320.2 x 60 = 19212 J = 19.212 kJ

370 kJ of heat is needed to vaporize 1 kg of liquid oxygen. Therefore, for the heat input of 19.212 kJ/min,

rate of oxygen becoming vapor = 19.212/370 = 0.0519 kg/min