Kinetics of Thermal Decomposition of N2O

Establish the kinetics of the thermal decomposition of Nitrous oxide from the following data and find the reaction rate at 990^oC and an initial pressure of 200 mm Hg.

t, min		20	53	100

% decomposition	23	50	73

Conversion (X_A) of Nitrous oxide (A) for various time values are given are given.

We shall test the date for first order, second order kinetics by integral method of analysis.

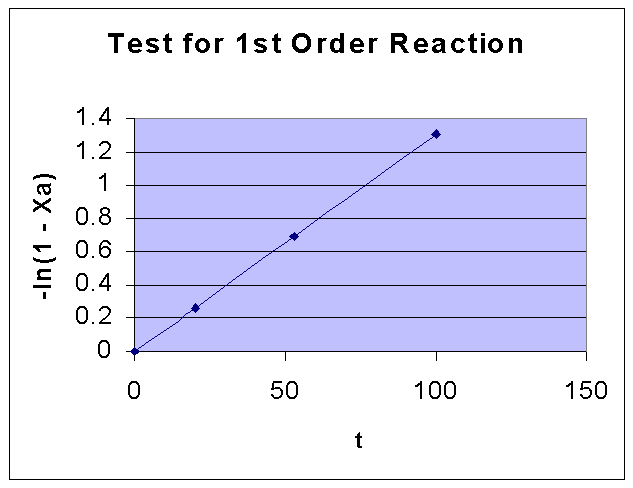
For a first order reaction, -ln(1 - X_A) vs. t is a straight line.

t, min	20	53	100

XA	0.23	0.50	0.73

From the above data the following graph is drawn:

For a second order reaction,

X_A/(C_Ao (1- X_A) ) = kt

i.e., X_A/(1 - X_A) vs. t is a straight line

From the above data the following graph is drawn:

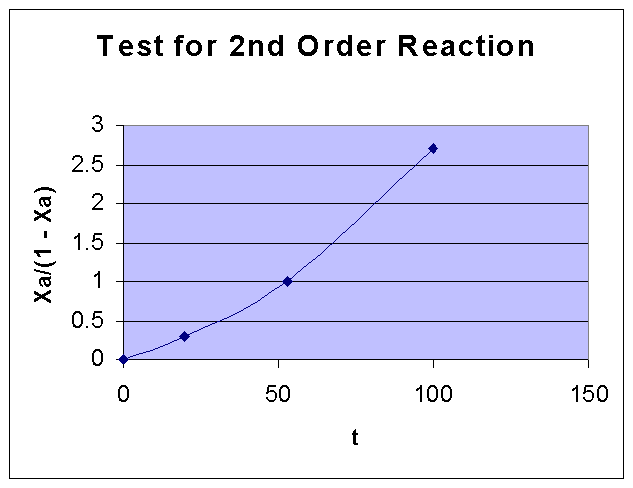
By comparing the two graphs, it can be seen that First order kinetics is well fiiting the given data. Fisrt order rate constant k is obtained from the slope of the first order data graph, and it is = 0.0131 sec^-1.

Therefore, -r_A = kC_A = kC_Ao(1 - X_A) = kp_Ao(1 - X_A)/RT = (1 - X_A) x 0.0131 x (200/760) x 101325 /(8314 x (990 + 273)) = 3.327 x 10^-5(1 - X_A)

i.e., -r_A = 3.327 x 10^-5(1 - X_A)

where X_A is fractional decomposition of Nitrous oxide, and -r_A is the rate of decomposition of Nitrous oxide.