Rate Equation from PFR data

The following conversion data were obtained in a tubular flow reactor for the gas-phase pyrolysis of acetone at 520^oC and 1 atm.

CH₃COCH₃ -> CH₃=C=O + CH₄

Flow rate, g/hr 	130	50	21	10.8
Conversion of acetone	0.05	0.13	0.24	0.35

The reactor was 80 cm long with 3.3 cm inner diameter. What rate equation is suggested?

Calculations:

Volume of reactor = (π/4)D² L = 684 cm³ = 0.684 lit

Molecular weight of acetone = 12 + 3 + 12 + 16 + 12 + 3 = 58

The above flow rate data in g/hr are converted into gmol/hr, by dividing them with Molecular weight.

Flow rate, g/hr 130 50 21 10.8

Molal flow rate, gmol/hr (F_Ao) 2.2414 0.8621 0.3621 0.1862

Conversion of acetone (X_A) 0.05 0.13 0.24 0.35

For the (tubular flow) plug flow reactor the design equation is,

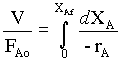
→ 1

C_Ao = p_Ao/RT = 1.01325 x 10^-5/(8314 x (273 + 520))

= 0.01537 kmol/m³ = 0.01537 gmol/lit

For the first order reaction, (variable density systems)

-r_A = kC_A = kC_Ao(1 - X_A)/(1 + ε_AX_A) → 2

substituting for -r_A from equn.2 in equn.1,

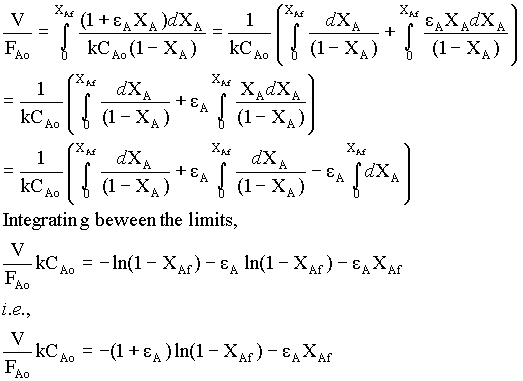
for the given gas-phase reaction, ε_A = (V_{XA = 1} - V_{XA = 0}) / V_{XA = 0} = (2 - 1)/1 = 1

Therefore,

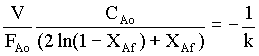
For the constant V and C_Ao,

F_Ao ( 2 ln(1 - X_Af) + X_Af) = -VC_Aok = constant. → 3

For second order reaction, (by Analytical integration)

k C_Ao² V/F_Ao = 2ε_A(1 + ε_A) ln(1- X_Af) + ε_A²X_Af + (ε_A + 1)² X_Af/(1 + X_Af)

For the given problem, ε_A = 1. Therefore,

(4 ln(1- X_Af) + X_Af + 4 X_Af/(1 + X_Af) ) F_Ao = k C_Ao² V = constant. → 4

We will check the above relations for various data available.

From the tabulated data, it could be seen that the second order mechanism is well fitting the data, than first order.

Therefore, the reaction is following second order.

k C_Ao² V = average of (4 ln(1- X_Af) + X_Af + 4 X_Af/(1 + X_Af) ) F_Ao for various F_Ao values

k C_Ao² V = 0.146429 (obtained by omitting the first data)

Therefore, k = 0.146429 / (0.01537² x 0.684) = 906.2 lit/(gmol.hr)

And the equation is,

Instead of analytical integration for 2^nd order reaction, we can use numerical integration (Simpson's 1/3 rule)

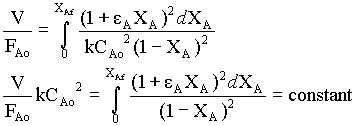
Numerical integration is obtained for the function

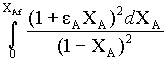
by taking 10 intervals.