Pascal's law for pressure at a point
The basic property of a static fluid is pressure. Pressure is familiar as a surface force exerted by a fluid against the walls of its container. Pressure also exists at every point within a volume of fluid. For a static fluid, as shown by the following analysis, pressure turns to be independent direction.
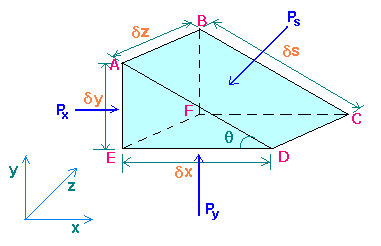
By considering the equilibrium of a small fluid element in the form of a triangular prism ABCDEF surrounding a point in the fluid, a relationship can be established between the pressures Px in the x direction, Py in the y direction, and Ps normal to any plane inclined at any angle q to the horizontal at this point.
Px is acting at right angle to ABEF, and Py at right angle to CDEF, similarly Ps at right angle to ABCD.
Since there can be no shearing forces for a fluid at rest, and there will be no accelerating forces, the sum of the forces in any direction must therefore, be zero. The forces acting are due to the pressures on the surrounding and the gravity force.
Force due to Px = Px x Area ABEF = Px \(\delta\)y\(\delta\)z
Horizontal component of force due to Ps = - (Ps x Area ABCD) sin(\(\theta\)) = - Ps \(\delta\)s\(\delta\) z \[\frac{\delta y}{\delta s}\] = -Ps\(\delta\)y\(\delta\)z
As Py has no component in the x direction, the element will be in equilibrium, if
Px\(\delta\)y\(\delta\)z + (-Ps\(\delta\)y\(\delta\)z) = 0
i.e. Px = Ps
Similarly in the y direction, force due to Py = Py\(\delta\)x\(\delta\)z
Component of force due to Ps = - (Ps x Area ABCD) cos(\(\theta\)) = - Ps\(\delta\)s\(\delta\)z \[\frac{\delta x}{\delta s}\] = - Ps\(\delta\)x\(\delta\)z
Force due to weight of element \[= - mg = - \rho Vg = \frac{- \rho \delta x \delta y \delta z}{2} g\]
Since \(\delta\)x, \(\delta\)y, and \(\delta\)z are very small quantities, \(\delta\)x\(\delta\)y\(\delta\)z is negligible in comparison with other two vertical force terms, and the equation reduces to,
Py = Ps
Therefore, Px = Py = Ps
i.e. pressure at a point is same in all directions. This is Pascal's law. This applies to fluid at rest.
Fine powdery solids resemble fluids in many respects but differs considerably in others. For one thing, a static mass of particulate solids, can support shear stresses of considerable magnitude and the pressure is not the same in all directions.
