Variation of pressure with elevation

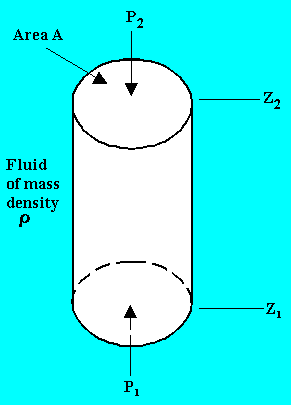
Consider a hypothetical differential cylindrical element of fluid of cross sectional area A and height (z₂ - z₁).

Upward force due to pressure P₁ on the element = P₁A

Downward force due to pressure P₂ on the element = P₂A

Force due to weight of the element = mg = \(\rho\)rA(z₂ - z₁)g

Equating the upward and downward forces,

P₁A = P₂A + \(\rho\)A(z₂ - z₁)g

P₂ - P₁ = - \(\rho\)g(z₂ - z₁)

Thus in any fluid under gravitational acceleration, pressure decreases, with increasing height z in the upward direction.

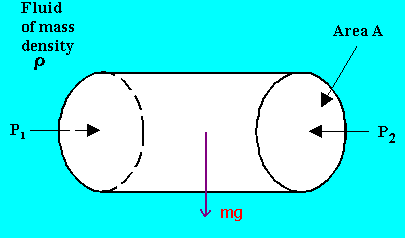
Equating the horizontal forces, P₁A = P₂A (i.e. some of the horizontal forces must be zero)

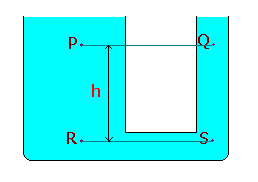
Pressures at the same level will be equal in a continuous body of fluid, even though there is no direct horizontal path between P and Q provided that P and Q are in the same continuous body of fluid.

We know that, P_R = P_S

P_R = P_P + \(\rho\)gh à 1

P_S = P_Q + \(\rho\)gh à 2

From equn.1 and 2, P_P = P_Q

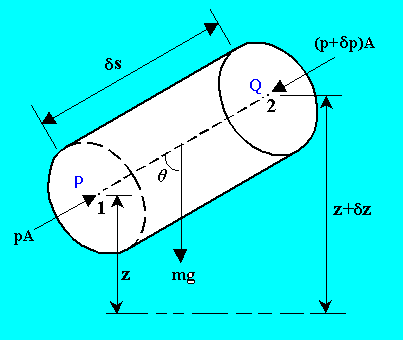
Resolving the forces along the axis PQ,

pA - (p + \(\delta\)p)A - \(\rho\)gA\(\delta\)ds cos(\(\theta\))= 0

\(\delta\)p = - \(\rho\)g\(\delta\)s cos(\(\theta\))

or in differential form,

\[\frac{dp}{ds}\] = - \(\rho\)gcos\(\theta\)

In the vertical z direction, q = 0.

Therefore,

\[\frac{dp}{dz} = -\rho g\]

This equation predicts a pressure decrease in the vertically upwards direction at a rate proportional to the local density.