U - tube Manometer with one leg enlarged
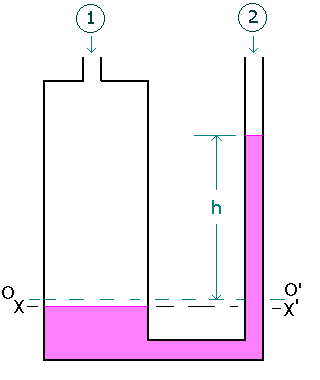
Industrially, the simple U - tube manometer has the disadvantage that the movement of the liquid in both the limbs must be read. By making the diameter of one leg large as compared with the other, it is possible to make the movement the large leg very small, so that it is only necessary to read the movement of the liquid in the narrow leg.
In figure, OO' represents the level of liquid surface when the pressure difference P1 - P2 is zero. Then when pressure is applied, the level in the right hand limb will rise a distance h vertically.
Volume of liquid transferred from left-hand leg to right-hand leg
= h(p/4)d2
where d is the diameter of smaller diameter leg. If D is the diameter of larger diameter leg, then, fall in level of left-hand leg
= Volume transferred/Area of left-hand leg
= (h(p/4)d2) / ((p/4)D2)
= h(d/D)2
For the left-hand leg, pressure at X , i.e. Px = P1 + rg(h+a) + rg h(d/D)2
For the right-hand leg, pressure at X', i.e. Px' = P2 + rga + rg(h + h(d/D)2)
For the equality of pressure at XX',
P1 + rg(h+a) + rg h(d/D)2 = P2 + rga + rmg(h + h(d/D)2)
P1 - P2 = rmg(h + h(d/D)2) - rgh - rg h(d/D)2
If D>>d then, the term h(d/D)2 will be negligible( i.e approximately about zero)
Then P1 - P2 = (rm - r)gh.
Where h is the manometer liquid rise in the right-hand leg.
If the fluid density is negligible compared with the manometric fluid density ( eg. the case for air as the fluid and water as manometric fluid ), then P1 - P2 = rm gh.