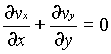Continuity Equation

Let us make the mass balance for a fluid element as shown below: (an open-faced cube)

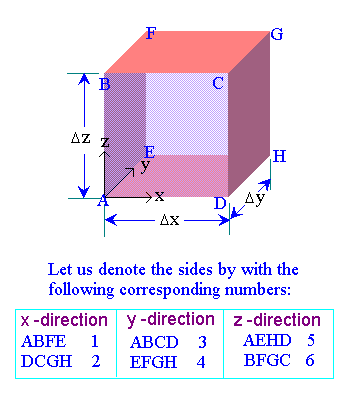
Mass balance:

Accumulation rate of mass in the system = all mass flow rates in - all mass flow rates out     --> 1

The mass in the system at any instant is r Dx Dy Dz. The flow into the system through face 1 is

and the flow out of the system through face 2 is

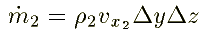
Similarly for the fcaes 3, 4, 5, and 6 are written as follows:

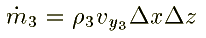
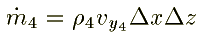
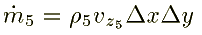
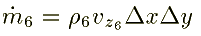
Substituting these quantities in equn.1, we get

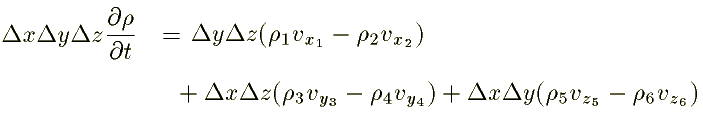
Dividing the above equation by Dx Dy Dz:

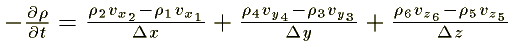
Now we let Dx, Dy, and Dz each approach zero simulaneously, so that the cube shrinks to a point. Taking the limit of the three ratios on the right-hand side of this equation, we get the partial derivatives.

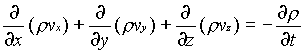
This is the continuity equation for every point in a fluid flow whether steady or unsteady , compressible or incompressible.

For steady, incompressible flow, the density r is constant and the equation simplifies to

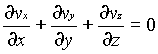
For two dimensional incompressible flow this will simplify still further to