Efflux Time
Efflux time - It is the time required for draining out the vessel contents. It is obtained by the application of Bernoulli equation by solving unsteady state mass balance equation.
The problem is to find the the efflux time (time needed to empty the vessel contents), for the given experimental setup consisting of Circular tank
(i) with Orifice opening at the bottom
(ii) with an exit pipe extending from the bottom of the tank
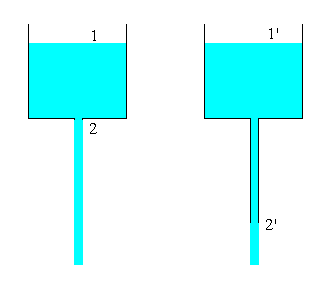
Time needed to empty the vessel (tefflux) can be found theoretically by unsteady state mass balance and steady state energy balance.
Mass Balance:
Rate of mass in - Rate of mass out = rate of change of mass accumulation
If there is no input, then
- rate of mass out = rate of change of mass accumulation
- mout = dm/dt
mout = volumetric flow rate x density = Ao v2 r
Rate of change of mass accumulation = rate of change of volume x density
=r dV/dt
where dV is the change in volume of water for a time interval of dt
Since V = area of tank x height of water = AT h,
and, dV = ATdh
Therefore,
Ao v2 r = AT r dh/dt à 1
v2 is obtained by making energy balance between the section 1 and 2:
p1 = 0 atm (g)
p2 = 0 atm (g)
v1 = 0 (negligible velocity compared to position 2)
Taking reference as position 2, (position 1 and 2 are in a continuous column of fluid)
z2 = 0
Therefore, Bernoulli equation reduces to
v22 = 2gz1
v2 = Ö (2gz1)
The height z2 - z1 can be taken as h. (water level with respect to position at any time t)
Therefore,
v2 = Ö (2gh) à 2
Substituting from Equn.2 for v2 in Equn.1,
Ö (2gh) = (AT/Ao) dh/dt
Separating the variables,
(AT/Ao) dh/Ö (2gh) = dt
Integrating between the limits z1 to z2 for a time of 0 to tefflux
tefflux = 2 AT [Ö z1 - Ö z2] / [AoÖ (2g)]
To account for the effect of contraction, Co is introduced; and the is modified as,
tefflux = 2 AT [Ö z1 - Ö z2] / [CoAoÖ (2g)]
Similar Equation can be derived for the tank with an exit pipe extending from the bottom.