Trajectory of a free jet

In a free jet the pressure is atmospheric throughout the trajectory.

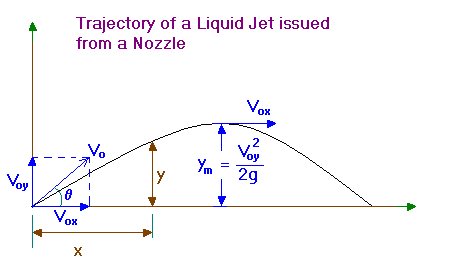
\[V_ox = V_o \cos \theta = constant = V_x\]

\[V_{oy} = V_o \sin \theta\]

\[x = V_{ox} t\]

\[y = V_{oy} t - \frac{gt^2}{2}\]

eliminating t gives,

\[y = x \frac{V_{oy}}{V_{ox}} - \frac {gx^2}{(2V{ox}^2)}\]

i.e,

\[y = x \tan \theta - \frac{gx^2}{(2V_o^2 \cos^2 \theta)}\]

This is the equation of the trajectory.

---------------

At the point of maximum elevation, V_y = 0 and application of Bernoulli’s law between the issue point of jet and the maximum elevation level,

\[\frac{V_o^2}{2g} = \frac{V_{ox}^2}{(2g)} + y_m\]

Since, \[\frac{V_o^2}{2g} = \frac{V_{ox}^2}{(2g)} + \frac{V_{oy}^2}{(2g)}\]

we get,

\[y_m = \frac{V_{oy}^2}{(2g)}\]