Trajectory of Jet issued from an orifice at the side of a tank opened to atmosphere

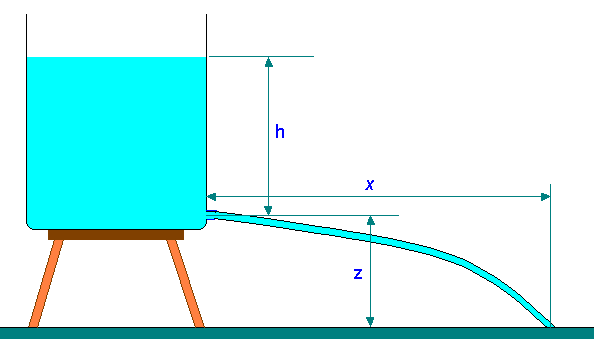
At the tip of the opening:

The horizontal component of jet velocity \[V_x = (2gh)^{0.5} =\frac{dx}{dt}\]

And the vertical component V_z = 0

One the jet is left the orifice, it is acted upon by gravitational forces. This makes the vertical component of velocity to equal ‘-gt’.

i.e., \[V_z = -gt =\frac{dz}{dt}\]

The horizontal and vertical distances covered in time ‘t’ are, obtained from integrating the above equations.

\[x = (2gh)^{0.5} t\]

and \[z = \frac{-gt^2}{2z}\]

And elimination of ‘t’ can be done as,

\[z = \frac{-g[\frac{x^2}{(2gh)}]}{2}\]

i.e,

\[z = \frac{-x^2}{(4h)}\]

Let us take downward direction as positive z. Then

\[x = 2(hz)^{0.5}\]