Incompressible - Turbulent flow in circular pipes

The head loss in turbulent flow in a circular pipe is given by,

h_f = 2fLv² / D = Dp / r

where f is the friction factor, defined as

f = t_w / (rv²/2)

where t_w is wall shear stress.

The value of friction factor f depends on the factors such as velocity (v) , pipe diameter (D) , density of fluid (r) , viscosity of fluid (m) and absolute roughness (k) of the pipe.

These variables are grouped as the dimensional numbers NRe and k/D

Where NRe = Dvr/m = Reynolds number

and k/D is the relative roughness of the pipe.

Blasisus, in 1913 was, the first to propose an accurate empirical relation for the friction factor in turbulent flow in smooth pipes, namely

f = 0.079 / NRe^0.25

This expression yields results for head loss to + 5 percent for smooth pipes at Reynolds numbers up to 100000.

For rough pipes, Nikuradse, in 1933, proved the validity of f dependence on the relative roughness ratio k/D by investigating the head loss in a number of pipes which had been treated internally with a coating of sand particles whose size could be varied.

Thus, the calculation of losses in turbulent pipe flow is dependent on the use of empirical results and the most common reference source is the Moody chart, which is a logarithmic plot of f vs. NRe for a range of k/D values. A typical Moody chart is presented as figure.

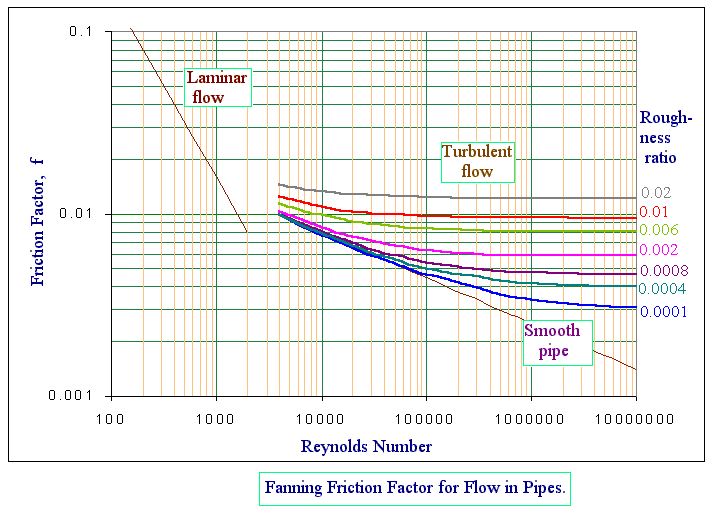
There are a number of distinct regions in the chart.

1. The straight line labeled 'laminar flow', representing f = 16/NRe, is a graphical representation of the Poiseuille equation. The above equation plots as a straight line of slope -1 on a log-log plot and is independent of the pipe surface roughness.
2. For values of k/D < 0.001 the rough pipe curves approach the Blasius smooth pipe curve.