Section: Energy Balance Calculations | Process Calculations - Video Lectures

Energy balance calculations for processes with no chemical reaction, specific heat, latent heat. Energy balance calculations for processes with single / multiple reactions. Heat of reaction from heat of formation, heat of combustion. Adiabatic reaction temperature.

Select activity Checklist

Checklist

Students must

Mark as done
Select activity Theory with Examples

Theory with Examples Page

Not available unless: You are a(n) Student
Select activity Questions - Energy Balance Calculations

Questions - Energy Balance Calculations Book
Select activity Steam Mixing

Steam Mixing Page

Not available unless: You are a(n) Student
Select activity Adiabatic Mixing of Steam

Adiabatic Mixing of Steam Page

Not available unless: You are a(n) Student
Select activity Temperature vs Time Curve for Heating of Water

Temperature vs Time Curve for Heating of Water Page

Not available unless: You are a(n) Student
Select activity Heat of Formation from Heat of Combustion Data

Heat of Formation from Heat of Combustion Data Page

Not available unless: You are a(n) Student
Select activity Heat of Reaction from Heat of Combustion

Heat of Reaction from Heat of Combustion Page

Not available unless: You are a(n) Student
Select activity Heat Released from Reaction

Heat Released from Reaction Page

Not available unless: You are a(n) Student
Select activity Adiabatic Flame Temperature of Natural Gas Combustion
Adiabatic Flame Temperature of Natural Gas Combustion Page
A natural gas containing 82 mole% \(\ce{CH4}\) and the balance \(\ce{C2H6}\) is burned with 20% excess air in a boiler furnace. The fuel gas enters the furnace at 298 K, and the air is preheated to 423 K.

The heat capacities of the stack gas components may be assumed to have the following constant values in J/(mol.K): \(\ce{CO2}\) = 50; \(\ce{H2O(g)}\) = 38.5; \(\ce{O2}\) = 33.1; \(\ce{N2}\) = 31.3.

Standard heat of formation values in kJ/mol are as follows: \(\ce{CH4}\) = \(-74.85\); \(\ce{C2H6}\) = \(-84.67\); \(\ce{CO2}\) = \(-393.50\); \(\ce{H2O(g)}\) = \(-241.83\).

Assuming complete combustion of the fuel, calculate the adiabatic flame temperature.

How would the flame temperature change if the percent excess air were increased?

How would the flame temperature change if the percent methane in the fuel were increased?
Not available unless: You are a(n) Student
Select activity Maximum Allowable Conversion of Exothermic Reaction

Maximum Allowable Conversion of Exothermic Reaction Page

2002-13-pc
Ammonia is produced by the following reaction\[ \text{N}_2 + 3\text{H}_2 \rightleftharpoons 2\text{NH}_3 \]In a commercial process for ammonia production, the feed to an adiabatic reactor contains 1 kmol/s of nitrogen and stoichiometric amount of hydrogen at 700 K. What is the maximum allowable conversion (in percentage) in the reactor, if the adiabatic temperature rise across the reactor should not exceed 100 K. Assume the feed and product streams to be ideal gas mixtures. The heat of reaction at 700 K for the above reaction is calculated to be -94.2 kJ/mol. Mean molar heat capacities (\(C_P\)), in the range 700 - 800 K, are 0.03, 0.0289 and 0.0492 kJ/(mol.K) for nitrogen, hydrogen and ammonia respectively.

Not available unless: You are a(n) Student
Select activity Heat Loss from the Combustion System

Heat Loss from the Combustion System Page

2014-42-pc

Carbon monoxide (CO) is burnt in presence of 200% excess pure oxygen and the flame temperature achieved is 2298 K. The inlet streams are at 25^oC. The standard heat of formation (at 25^oC) of CO and CO₂ are -110 kJ.mol^-1 and -390 kJ.mol^-1, respectively. The heat capacities (in J.mol^-1.K^-1) of the components are \[ C_{P_{\text{O}_2}}= 25 + 14\times10^{-3}T \qquad C_{P_{\text{CO}_2}} = 25 + 42\times10^{-3}T \] where, \(T\) is the temperature in K. The heat loss (in kJ) per mole of CO burnt is _______.

Not available unless: You are a(n) Student

Isothermal Operation of Combustor to Convert Carbon and CO2 to CO Page

1997-13-pc

A feed at 1298 K, consisting of flue gas (\(\ce {CO2}\), \(\ce {O2}\) and \(\ce {N2}\)) and air, is passed through a bed of pure carbon. The reactions that occur both go to completion. \[ \begin {align*} \ce {CO2(g)} + \ce {C(s)} &\rightarrow 2\ce {CO(g)}, \quad \Delta H^\circ _R \text { at 298 K = 170 kJ/mol} \\
\ce {O2(g)} + 2\ce {C(s)} &\rightarrow 2\ce {CO(g)}, \quad \Delta H^\circ _R \text { at 298 K = \(-\)220.4 kJ/mol} \end {align*} \] The combustor is adiabatic and the product gases exit at 1298 K. Calculate the required moles of \(\ce {CO2}\) per mole of \(\ce {O2}\) in the feed stream, so that the net heat generated is zero and the bed temperature remains constant at 1298 K.
Data: Mean molar heat capacities, \(C_{Pm}\)

Substance	\(\ce{C}\)	\(\ce{O2}\)	\(\ce{CO}\)	\(\ce{CO2}\)
\(C_{Pm}\) (kJ/[mol.K])	0.02	0.03	0.03	0.05

Select activity Calorific Value of Fuels

Calorific Value of Fuels Page

Not available unless: You are a(n) Student
Select activity Heat Transferred from Reactor

Heat Transferred from Reactor Page

Not available unless: You are a(n) Student
Select activity Adiabatic Combustion of Methane

Adiabatic Combustion of Methane Page

Not available unless: You are a(n) Student
Select activity Heat Released from Combustion of CO

Heat Released from Combustion of CO Page

Not available unless: You are a(n) Student
Select activity Rate of Heat Removal from Ammonia Oxidizer

Rate of Heat Removal from Ammonia Oxidizer Page

Not available unless: You are a(n) Student

Heat Removed from Ammonia Oxidizer - Multiple Reactions Page

Ammonia is oxidized with air to form nitric oxide in the first step of the production of nitric acid. Tow principal reactions occur: \[ \begin{align*} \ce{4NH3} + \ce{5O2} &\rightarrow \ce{4NO} + \ce{6H2O} \\ \ce{2NH3} + \ce{2/3 O2} &\rightarrow \ce{N2} + \ce{3H2O} \end{align*}\]

A flowchart of the reactor follows.

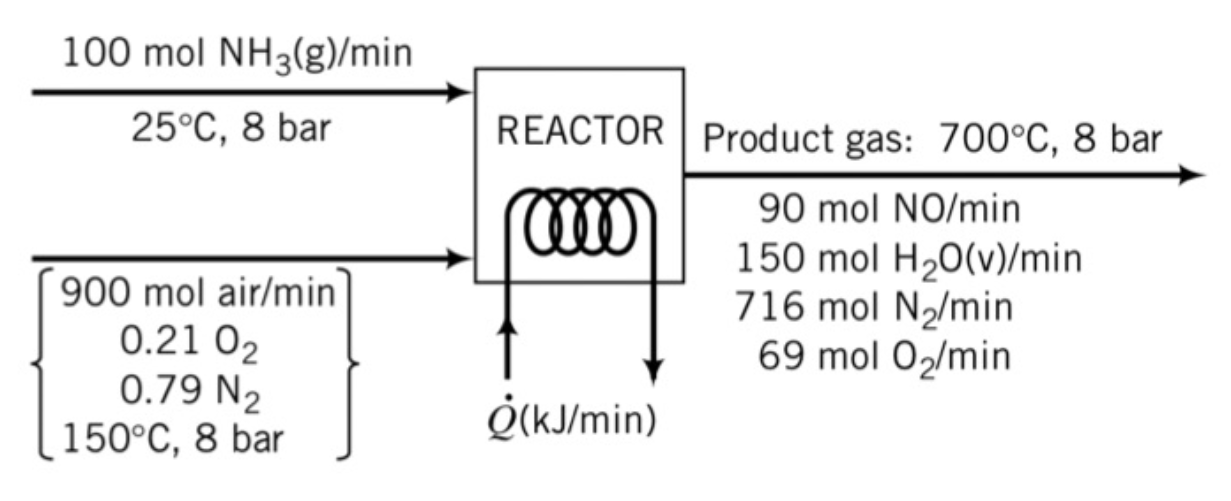
Mean specific heat and standard heat of formation of components are given in the table:

Component	C_pm (25 to 150^oC) J/(mol.^oC)	C_pm (25 to 700^oC) J/(mol.^oC)	\(\Delta H_f^\circ\) kJ/mol
NH₃(g)	37.8	46.0	-46.19
NO(g)	30.2	32.0	90.37
H₂O(g)	34.1	36.9	-241.83
O₂(g)	30.1	32.4	-
N₂(g)	29.2	30.5	-

Calculate the required heat transfer to or from the reactor in kW.
Heat is to be ______ (removed from the reactor / added to the reactor)

Not available unless: You are a(n) Student

Select activity Temperature of Ammonia Oxidizer

Temperature of Ammonia Oxidizer Page

Not available unless: You are a(n) Student
Select activity Energy Balance for Production of Acetylene from Methane

Energy Balance for Production of Acetylene from Methane Page

Students must

Mark as done
Select activity Energy Balance for Production of Acetylene - Another Explanation

Energy Balance for Production of Acetylene - Another Explanation Page

Not available unless: You are a(n) Student
Select activity Exit Temperature of Flue Gas

Exit Temperature of Flue Gas Page

Not available unless: You are a(n) Student
Select activity Excess Air and Adiabatic Flame Temperature

Excess Air and Adiabatic Flame Temperature Page

Not available unless: You are a(n) Student

Section outline