Process Control - Video Lectures
Section outline
-
-
Modeling of Temperature Variation in Water Tank Page2003-76-ctrlWater is entering a storage tank at a temperature \(T_0\) and flow rate \(Q_0\) and leaving at a flow rate \(Q\) and temperature \(T\). There are negligible heat losses in the tank. The area of cross section of the tank is \(A_c\). The model that describes the dynamic variation of water temperature in the tank with time is given as
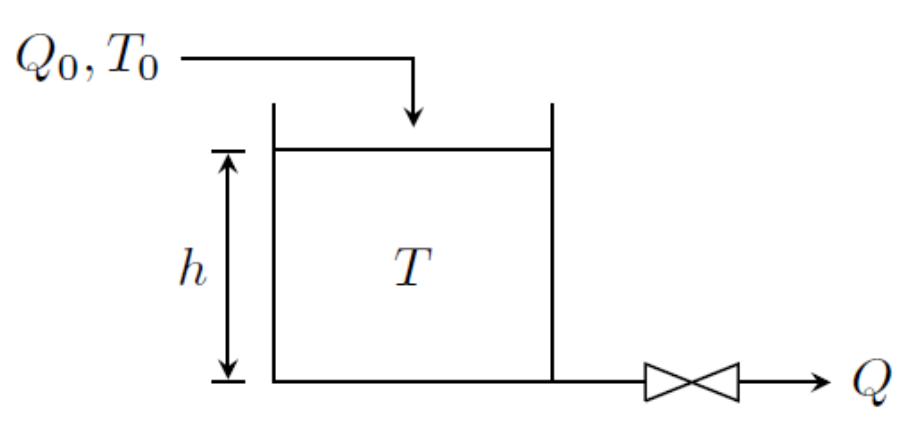
- \(Q_0(T_0-T) = A_ch\dfrac{dT}{dt}\)
- \(Q_0T_0-QT = A_ch\dfrac{dT}{dt}\)
- \(Q(T_0-T) = A_ch\dfrac{dT}{dt}\)
- \(Q(T_0-T) = A_c\dfrac{d(Th)}{dt}\)
-
-
Dynamic Model of a Stirred Tank Mixer Page
-
Dynamic Model of a Stirred Tank Heater Page
-
Dynamic Model of Stirred Tank Heater of Variable Volume Page
-
Dynamic Model of Interacting Tanks Page
