02 - First Order Systems

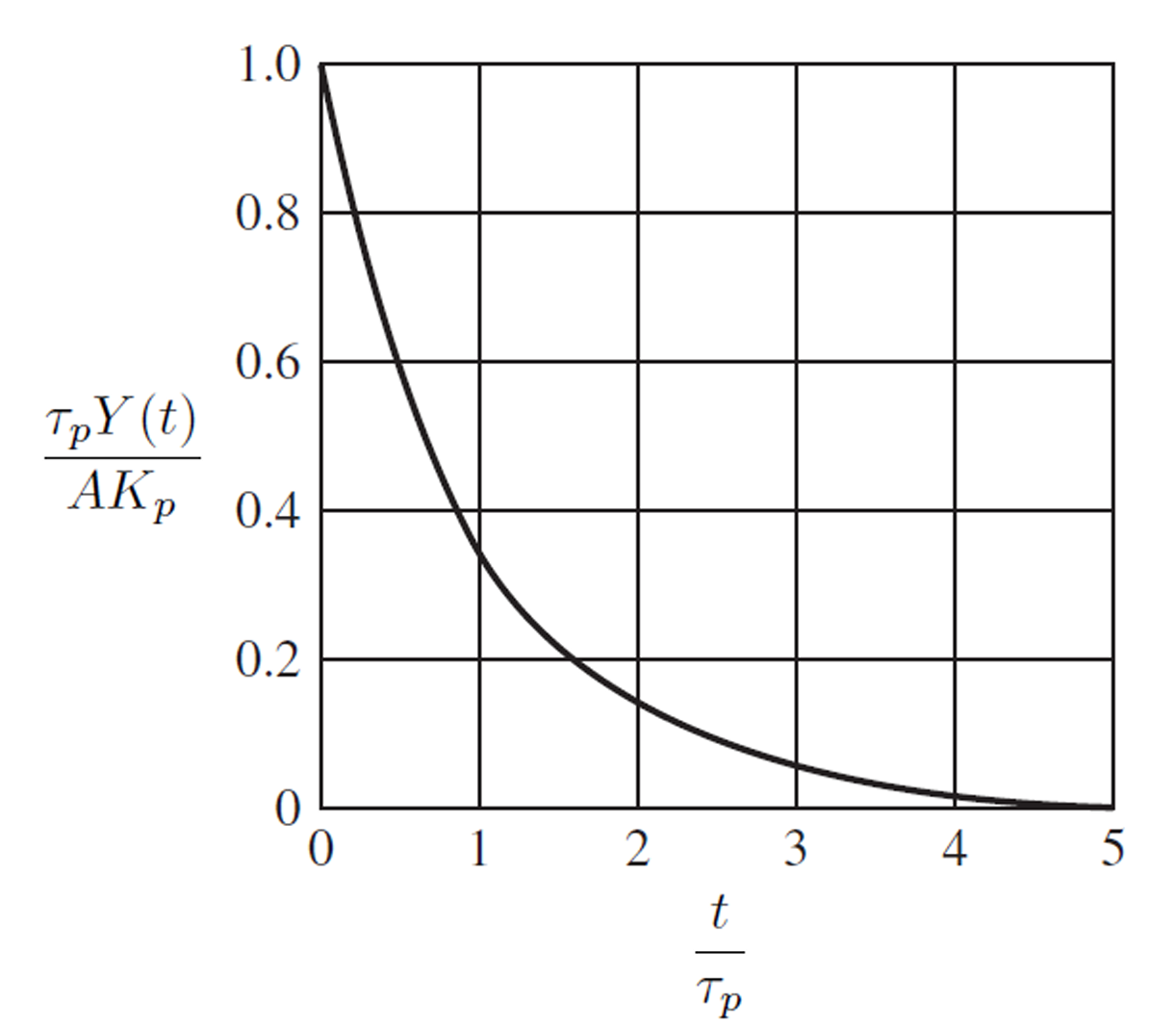
\[G_p(s) = \frac{Y(s)}{X(s)} = \frac{K_p}{\tau_p s + 1}\] For impulse input of magnitude 1, \(X(s)=1\). i.e., unit impulse.

For impulse input of magnitude \(A\), \(X(t)=A\delta(t)\), and \(X(s)=A\).

This leads to \[Y(s) = \frac{AK_p}{\tau_p s+1} = \frac{AK_p/\tau_p}{s+1/\tau_p}\] Taking \(\mathcal{L}^{-1}\), \[Y(t) = \frac{AK_p}{\tau_p}(e^{-t/\tau_p})\]