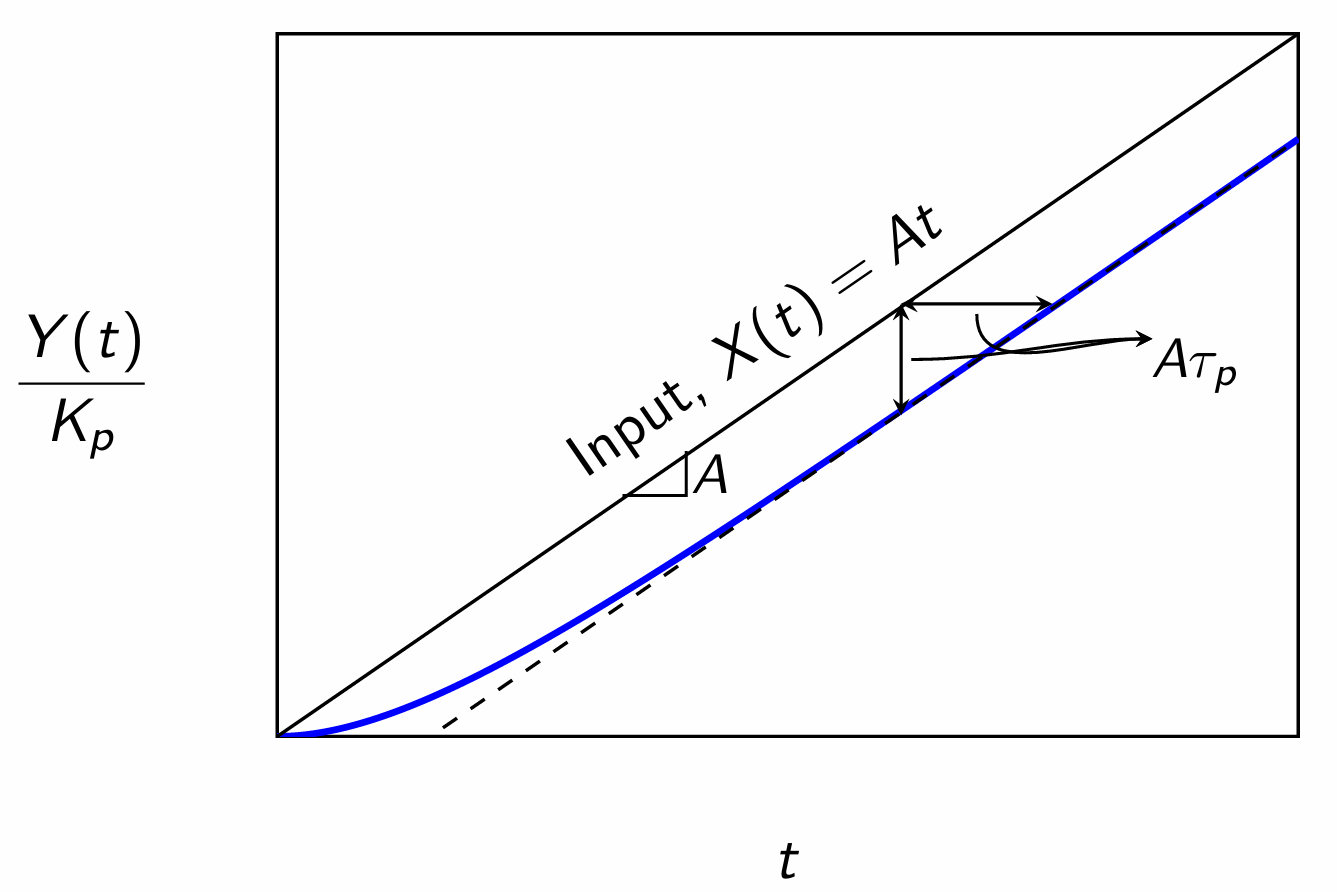
22. Response of First Order System to Ramp Input

First order system: \[\frac{Y(s)}{X(s)} = \frac{K_p}{\tau_p s+1}\] Input: \[X(t) = At \qquad \Longrightarrow \quad X(s) = \frac{A}{s^2}\] Therefore, \[Y(s) = \frac{A}{s^2}\frac{K_p}{\tau_p s+1}\] Expanding by partial fractions, \[\frac{C_1}{s} + \frac{C_2}{s^2} + \frac{C_3}{\tau_p s +1} = \frac{AK_p}{s^2(\tau_p s+1)}\] Solving for \(C_1,C_2,C_3\) we get \[Y(s) = AK_p\left(\frac{1}{s^2}-\frac{\tau_p}{s} + \frac{\tau_p}{s+1/\tau_p} \right)\]

Taking inverse Laplace transform, and grouping the terms, we get \[Y(t) = AK_p\left[t-\tau_p\left(1-e^{-t/\tau_p}\right) \right]\]