Heat Transfer - Video Lectures
Section outline
-
-
Skin Temperature from Heat Loss Data PageCengel-3-26Consider a person standing in a room at 20oC with an exposed surface area of 1.7 m2. The deep body temperature of the human body is 37oC, and the thermal conductivity of the human tissue near the skin is about 0.3 W/(m.oC). The body is losing heat at a rate of 150 W by natural convection and radiation to the surroundings. Taking the body temperature 0.5 cm beneath the skin to be 37oC, determine the skin temperature of the person.
______ oC (round off to 1 decimal place).
-
Surface Temperature of Slab Page
-
Heat Conduction through Composite Flat Wall Page
-
Thermal Contact Resistance Page
-
ME-2022-S1-64Consider a solid slab (thermal conductivity, \(k\) = 10 W/[m.K]) with thickness 0.2 m and of infinite extent in the other two directions as shown in the figure. Surface 2 , at 300 K, is exposed to a fluid flow at a free stream temperature (\(T_\infty\)) of 293 K, with a convective heat transfer coefficient (\(h\)) of 100 W/(m2.K). Surface 2 is opaque, diffuse and gray with an emissivity (\(\varepsilon\)) of 0.5 and exchanges heat by radiation with very large surroundings at 0 K. Radiative heat transfer inside the solid slab is neglected. The Stefan-Boltzmann constant is \(5.67\times10^{-8}\) W/(m2.K4). The temperature \(T_1\) of surface 1 of the slab, under steady-state conditions, is ______ K (round off to the nearest integer).
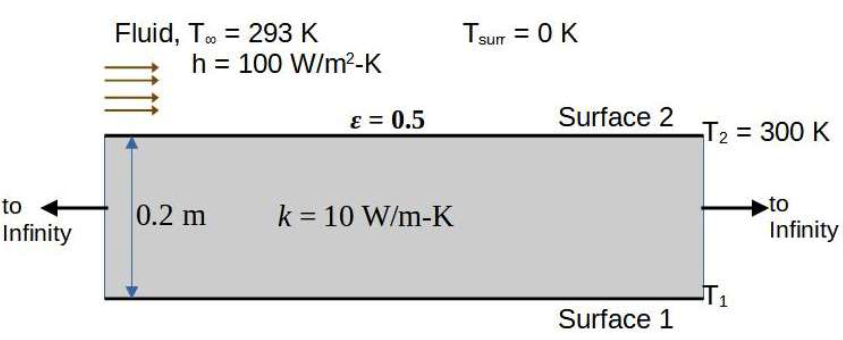
-
Surface Temperatures of Window Glass PageIncropera6E-3-2The rear window of an automobile is defogged by passing warm air over its inner surface. If the warm air is at \(T_{\infty i}\) = 40oC and the corresponding convection coefficient is \(h_i\) = 30 W/(m2.K), what are the inner and outer surface temperatures of 4 mm thick window glass (\(k\) = 1.4 W/[m.K]), if the outside ambient air is \(T_{\infty o}\) = -10oC and the associated convection coefficient is \(h_o\) = 65 W/(m2.K).
- Inner surface temperature of window glass = __________ oC
- Outer surface temperature of window glass = __________ oC
-
Heat Loss from Cylindrical Surface Page
-
Heat Transfer through Thin-walled Cylindrical Pipe Page
-
Thickness of Insulation of Refrigerator PageCengel-3-35The wall of a refrigerator is constructed of fiberglass insulation (\(k\) = 0.035 W/[m.oC]) sandwiched between two layers of 1 mm thick sheet metal (\(k\) = 15.1 W/[m.oC]). The refrigerated space is maintained at 3oC, and the average heat transfer coefficients at the inner and outer surfaces of the wall are 4 W/(m2.oC) and 9 W/(m2.oC), respectively.
The kitchen temperature averages 25oC. It is observed that condensation occurs on the outer surfaces of the refrigerator when the temperature of the outer surface drops to 20oC. Determine the minimum thickness of fiberglass insulation that needs to be used in the wall in order to avoid condensation on the outer surfaces. ______ mm (round off to 1 decimal place).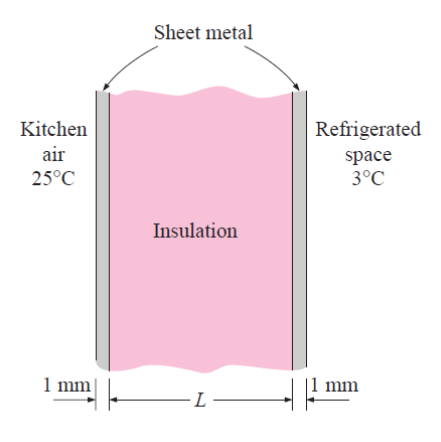
-
Thermal Conductivity and Temperature Gradient Page
-
Effective Thermal Conductivity of Composite Page
-
Heat Conduction through Truncated Cone Page
-
Heat Conduction through Flat Plate with Varying Thermal Conductivity Page
-
Heat Transfer in Series-Parallel Resistances PageCengel-3-57Consider a 5 m high, 8 m long, and 22 cm thick wall whose representative cross section is as given in the figure. The thermal conductivities of various materials used, in W/(m.oC), are \(k_A = k_F = 2; \ k_B = 8, \ k_C = 20, \ k_D = 15\), and \(k_E=35\). The left and right surfaces of the wall are maintained at uniform temperatures of 300oC and 100oC, respectively.
Assuming heat transfer through the wall to be one-dimensional, determine: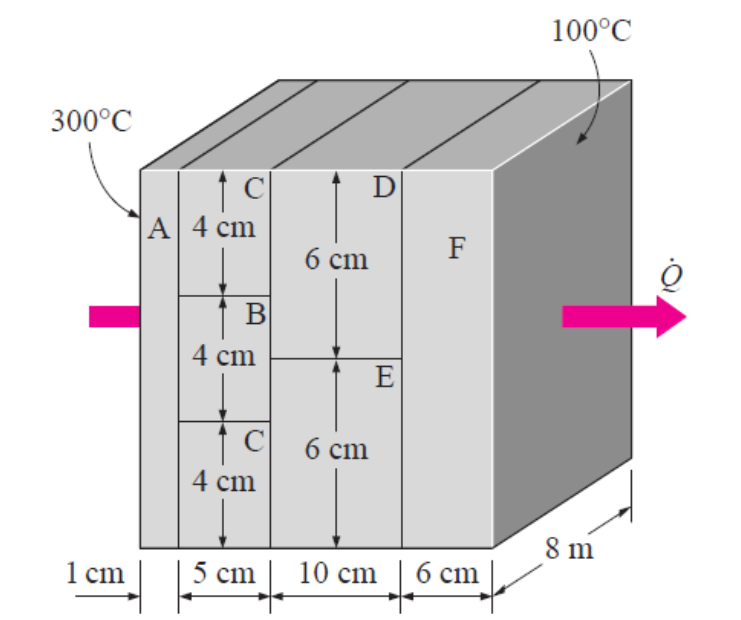
- the rate of heat transfer through the wall = ______ \(\times10^5\) W
- the temperature at the point where the sections \(B,D\), and \(E\) meet = ______ oC
- the temperature drop across section \(F\) = ______ oC
-
Heat Transfer through Series-Parallel Resistances Page
-
Heat Transfer through Cylindrical Insulated Pipe PageIncropera6E-3-52Steam flowing through a long, thin-walled pipe maintains the pipe wall at a uniform temperature of 500 K. The pipe is covered with an insulation blanket comprised of two different materials, \(A\) and \(B\).
The interface between the two materials may be assumed to have an infinite contact resistance, and the entire outer surface is exposed to air for which \(T_\infty\) = 300 K and \(h\) = 25 W/(m2.K). For the prescribed conditions,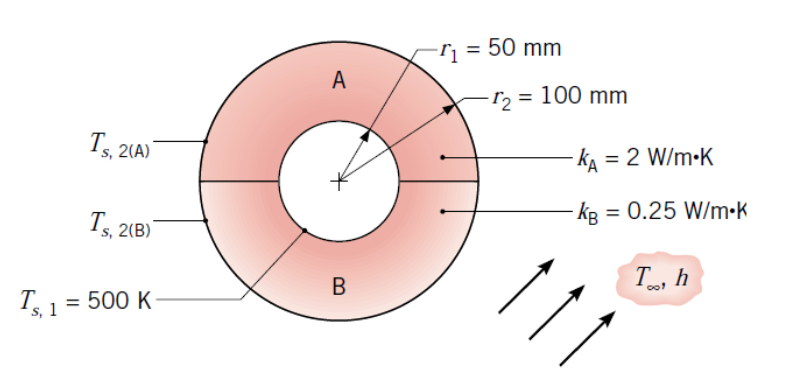
- what is the total heat loss from the pipe per meter length? ________ W (round off to integer)
- what are the outer surface temperatures \(T_{s2A}\)? _______ K, \(T_{s2B}\)? _______ K
-
Heat Transfer through Spherical Insulation PageIncropera6E-3-60A spherical vessel used as a reactor for producing pharmaceuticals has a 10 mm thick stainless steel wall (\(k\) = 17 W/[m.K]) and an inner diameter of 1 m. The exterior surface of the vessel is exposed to ambient air (\(T_\infty\) = 25oC) for which a convection coefficient of 6 W/(m2.K) may be assumed.
- During steady-state operation, an inner surface temperature of 50oC is maintained by energy generated within the reactor. What is the heat loss from the vessel? ______ W (round off to integer)
- If a 20 mm thick layer of fiberglass insulation (\(k\) = 0.040 W/[m.K]) is applied to the exterior of the vessel and the rate of thermal energy generation is unchanged, what is the inner surface temperature of the vessel? ______ oC (round off to 1 decimal place).
-
Spherical Tank with Insulation Page
-
Heat Loss due to Addition of Insulation to Spherical Ball PageCengel-3-91A 5 mm diameter spherical ball at 50oC is covered by a 1 mm thick plastic insulation \(k\) = 0.13 W/(m.oC). The ball is exposed to a medium at 15oC, with a combined convection and radiation heat transfer coefficient of 20 W/(m2.oC). Determine if the plastic insulation on the ball will lead to increasing or decreasing the heat loss from the ball.
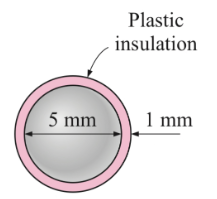
- increase the heat loss
- decrease the heat loss
- no change in heat loss
-
Surface Temperature of Insulated Wire PageCengel-3-88A 2 mm diameter and 10 m long electric wire is tightly wrapped with a 1 mm thick plastic cover whose thermal conductivity is \(k\) = 0.15 W/(m.oC). Electrical measurements indicate that a current of 10 A passes through the wire and there is a voltage drop of 8 V along the wire.

If the insulated wire is exposed to a medium at \(T_\infty\) = 30oC with a heat transfer coefficient of \(h\) = 24 W/(m2.oC), determine the temperature at the interface of the wire and the plastic cover in steady operation. _____ oC.
Also determine if doubling the thickness of the plastic cover will increase or decrease this interface temperature. _____ (decrease / increase)
-
Critical Thickness of Insulation and Heat Loss PageIncropera6E-3-53A bakelite coating (thermal conductivity = 1.4 W/[m.K]) is to be used with a 10 mm diameter conducting rod, whose surface is maintained at 200oC by passage of an electrical current. The rod is in a fluid at 25oC, and the convection coefficient is 140 W/(m2.K).
- What is the critical radius associated with the coating?
- What is the heat transfer rate (W) per meter length for the bare rod? and for the rod with a coating of bakelite that corresponds to the critical radius?
- How much should be thickness of bakelite to reduce the heat transfer associated with the bare rod by 25%?
-
Heat Loss from Spherical Surface - With and Without Insulation Page
-
k and q from Steady-state Temperature Distribution Page
-
dT/dx for Flat Wall with Variable Conductivity Page
-
Three-dimensional Heat Conduction Equation Page
